Our Covid-19 self-isolation regimen has produced some odd moments, like the time I stumbled into the living room and found my wife watching a nerdy show about mathematics. I had to rub my eyes and persuade myself I hadn’t inadvertently slipped on some cosmic foam and landed in an alternate universe. The nerdy show is Connections on Netflix produced and hosted by Latif Nasser. The episode in question is Digits which tells the story of Benford’s Law.
The counterintuitive idea behind Benford’s Law is that if you take a given data set of numbers (e.g. all the street addresses in a city), the lowest first digit (1) occurs more frequently than any other, the 2nd lowest (2) occurs more frequently than any other except 1, and so on … We tend to think the distribution of first digits in any given data set will be equal; there will be as many ones as eights. However, an empirical analysis of data sets demonstrates again and again that there are far more ones in our universe than any other number.
Benford’s Law is a mathematical description of that observation. It has nothing to say about why this is the case. In some instances, the why is self-evident. For example, in the case of municipal street addresses, short streets will have single and double digit address numbers with an equal distribution of first digits for the first 99 addresses. Slightly longer streets will have 3-digit address numbers each with one as the first digit for the next 100 addresses. Even longer streets will have 3-digit address numbers each with two as the first digit for the next 100 addresses. And so on. But most municipal streets are shorter, in the equal distribution range or one-weighted range. So it’s obvious that there will be more ones as a first digit than any other number.
It turns out Benford’s Law has practical applications. Forensic accountants can use it as a tool to alert them to possible fraud or tax evasion. It doesn’t definitively prove fraud or tax evasion, but it reliably alerts as to the possibility. It also has a practical application in digital photography in the detection of image manipulation.
The colour value of each pixel in a jpg image is expressed as a set of 3 hexadecimal numbers, one for each of red, green, and blue. (Benford’s Law provides a distribution in base 16 just as it does in base 10.) Most photographers and digital designers know that when you resave a jpg, the process of compressing an already compressed image produces digital artifacts that become more pronounced with each resave. What they may not know—and what I certainly didn’t know until now—is that resaving a jpg also skews the distribution of numerical values associated with the jpg’s hexadecimal colour values so that it violates Benford’s Law. We might not be able to detect these changes just by looking at the image, but an application that treats the colour values numerically can easily detect them. So, let’s say you have a stock image of the White House and you want to insert an image of the POTUS doing a cartwheel across the front lawn. A casual observer may find your image convincing, but the fact that you’ve had to mash together at least two images and have had to resave the result at least once guarantees that your manipulation can be detected when brought face to face with Benford’s Law.
Then I wondered if there is a way to test Benford’s Law using personal data unique to my photographic habits. I maintain a handwritten log. Not exactly a high-tech habit. Every time I have a gig or am out with my camera, I record where I was, what I was doing, what I shot, and total number of exposures. Does my record of number of exposures conform to Benford’s Law? I went back two years—246 entries with usable numerical values—and I tabulated the first digit of each entry to produce the following table:
| Digit | Total Times as 1st Digit | Percentage (of 246) |
| 1 | 85 | 34 |
| 2 | 51 | 21 |
| 3 | 27 | 11 |
| 4 | 19 | 8 |
| 5 | 13 | 5 |
| 6 | 10 | 4 |
| 7 | 17 | 7 |
| 8 | 14 | 6 |
| 9 | 10 | 4 |
From this data, I produced a bar chart with my percentage values (pink) displayed beside the Benford’s Law percentage values (grey). The result (surprising to my mind) is that the first digit from the number of photos I shoot each time I take up my camera roughly coincides with the numbers predicted by Benford’s Law. I account for the minor variances by the fact that my data sample size isn’t large enough. If I were to draw on data from 10 years instead of 2, I expect the results would be more in line with Benford’s Law.
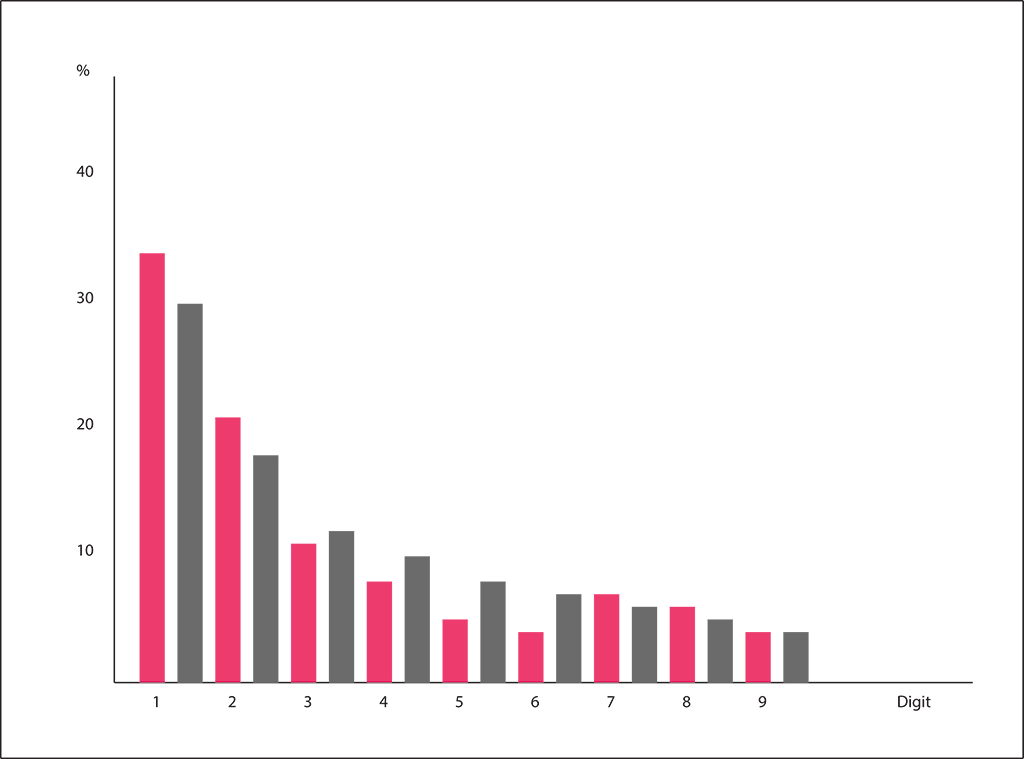
I say the result is “surprising to my mind” because I would have expected a purely random distribution. Any time I take up my camera, there is no intentionality behind how many exposures I shoot or when I stop. So it seems the numbers should produce random results. Why aren’t the numbers random? I think the rationale here is similar to the rationale I offered for the distribution of first digits on municipal street addresses. After a while, I get tired. It’s rare that I shoot 600 or 700 exposures at a time. Far more likely that I’ll shoot in the double digits where first digits are equally distributed or in the one hundreds where all the first digits are one.
And what use can I make of this information?
As far as I can discern, absolutely none. One of my favourite book titles is from a critical work on poetry called Beautiful and Pointless, by David Orr. Sometimes, that’s how I feel about photography, too. Some of the best images are beautiful and pointless. And as for blog posts…sometimes we need to revel in the simple pleasure of pointless endeavour.
